计算器指数函数怎么按(指数函数怎么用计算器算出来)

计算器指数函数是数学领域中的一个重要概念，它在许多应用中都扮演着重要角色。指数函数的形式为f(x) = a^x，其中a是常数且大于0且不等于1。指数函数在实际生活中有着广泛的应用，例如在经济增长模型、生物学中的人口增长模型以及放射性衰变等领域均有着重要的作用。

计算器指数函数的图像通常表现为一条曲线，其随着自变量x的增加而呈指数增长或指数衰减。这种特殊的增长模式使得指数函数在描述一些复杂的自然现象时具有独特的优势。下面我们将通过具体的例子来介绍指数函数的计算方法和应用。

指数函数的计算方法

指数函数的计算通常涉及到指数的运算、对数运算以及指数函数图像的绘制等内容。通过计算器，我们可以轻松地求解各种指数函数的取值，进而更好地理解指数函数的特性和规律。下面我们通过一个实际的例子来介绍指数函数的计算方法。

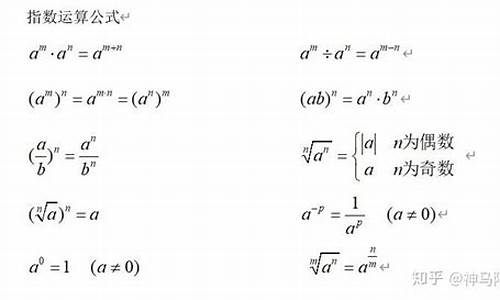
指数函数的应用

指数函数在实际生活中有着丰富的应用，其中包括经济增长模型、生物学中的人口增长模型以及放射性衰变等领域。通过指数函数，我们可以更好地描述和预测这些复杂的自然现象，为科学研究和生产实践提供重要的数学工具。

总结归纳

通过以上介绍，我们对计算器指数函数有了更深入的了解。指数函数作为数学中的重要概念，在实际中有着广泛的应用，其计算方法和应用领域的丰富性使得我们对指数函数有了更为全面和深入的认识。希望本文能够帮助读者更好地理解和应用指数函数的知识。

通过本文的介绍，相信读者对计算器指数函数有了更全面的了解。指数函数的计算方法和丰富的应用领域使得它在数学和现实生活中都具有重要意义。希望本文能够帮助读者更深入地理解和掌握指数函数的知识。